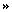Der Chemiker Alfred Lotka (1880-1949) und der Mathematiker Vito Volterra (1860-1940) forschten Mitte der 20er Jahre unabhängig voneinander mit Populationsdynamiken. Beide stießen etwa zur gleichen Zeit auf Regelmäßigkeiten in der Beziehung von Räuber-Beute-Populationen.

Der Zusammenhang zwischen Räuber-Beute ist dabei so zu verstehen: Der Räuber ernährt sich von der Beute. Die Anwendung der Regeln bzw. die Aussagekraft von echten Zahlen ist jedoch mit Vorsicht zu genießen. In der Theorie der Regeln gibt es nämlich nur diese eine idealisierte Räuber-Beute-Beziehung und keine anderen Einflussfaktoren. Das ist so in der Natur natürlich nicht gegeben. Dort findet man deutlich komplexere Wechselbeziehungen von Räuber und Beute Population: Denn ein Jäger wird in der Regel nie nur ein Tier jagen und ein Beutetier hat auch mehrere Fressfeinde.

 
Regel 1: Die Größe der Populationen von Räuber und Beute schwanken bei konstanten Bedingungen periodisch. Dabei folgt das Maxima der Räuberpopulation auf das Maxima der Beutepopulation.

Beispiel: Zu Beginn steigt die Populationsgröße der Hasen (Beute) deutlich an. Dadurch haben die Füchse (Räuber) ein höheres Nahrungsangebot und vermehren sich, sodass auch ihre Populationsgröße ansteigt. Irgendwann wird der Punkt erreicht, an dem die Füchse mehr Hasen fressen wie neue geboren werden. In der Folge sinkt die Hasenpopulation und damit auch das Nahrungsangebot der Füchse. Ihre Populationsgröße sinkt jetzt ebenfalls, nur eben leicht verzögert. Infolgedessen das es jetzt weniger Räuber gibt, kann sich die Hasenpopulation wieder erholen und es kommt zu einem Anstieg der Populationsgröße. Mehr Hasen bedeutet auch wieder mehr Nahrungsangebot für die Füchse, deren Population jetzt ebenfalls wieder ansteigt. Das Schema wiederholt sich.

 
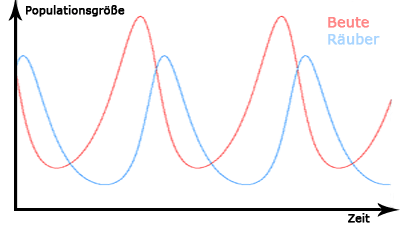
Regel 2: Die Populationsgrößen beider Einzelpopulationen schwanken konstant um einen festen Mittelwert.

Beispiel: Wie schon im ersten Beispiel oben nehmen wir Füchse und Hasen als Beispiel. Aufgrund des immer gleich ablaufenden Zyklus verändern sich auch die Extrema (sowohl die Hochpunkte, also die Maximalgrößen der Populationen, als auch die Tiefpunkte, dementsprechend die Minimalgrößen der Populationen) nicht wesentlich, sodass der Mittelwert konstant bleibt.
Demnach würde man wenn man mehrere Jahrabschnitte miteinander vergleicht (z.B. Jahr 1-3 mit Jahr 4-6) auch auf einen fast identischen Mittelwert kommen.

Übrigens: Der Mittelwert der Beutepopulation liegt stets über dem Mittelwert der Räuberpopulation. Umgekehrt wäre die Beutepopulation irgendwann komplett aufgefressen, weil ein Fuchs pro Zyklus deutlich mehr als nur einen Hasen frisst.

 
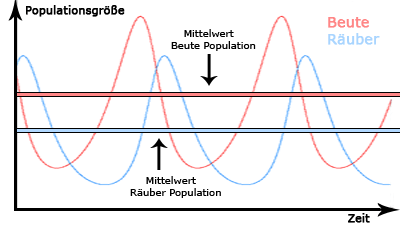
Regel 3: Werden Räuber-, als auch Beutepopulation gleichermaßen in ihrer Populationsgröße dezimiert, so erholt sich die Beutepopulation stets schneller als die Räuberpopulation.

Beispiel: Durch ein vom Menschen eingebrachtes Umweltgift stirbt ein Großteil der Hasen- und Fuchspopulation. Die Populationsgrößen beider sind jetzt ungefähr auf dem selben Niveau. Unabhängig der Größe der Räuberpopulation wächst die Beutepopulation immer schneller: Es werden mehr Hasen als Füchse geboren und die Beutepopulation kann sich zuerst wieder erholen. Hinzu kommt unmittelbar nach der beiderseitigen Dezimierung für die Füchse der Nachteil eines deutlich geringeren Nahrungsangebotes. Während sie auf die Zahl der Hasenpopulation angewiesen sind, um selbst zahlenmäßig wachsen zu können, fressen die Hasen einfach Gräser.